Cálculo de la MTF con ImageJ

En los aspectos para la evaluación de la calidad de la imagen digital, o más bien los dispositivos de captura de imagen, la MTF es una de las métricas más habituales para estimar la respuesta de una óptica.

La MTF o función de la transferencia de modulación de una lente nos indica la eficacia con la que una lente transfiere las variaciones en la luminosidad de una escena hasta el plano focal (detalle) y como esta varía en función de la frecuencia espacial (finura del detalle)

Aun que a lo largo de la historia de la imagen digital se han planteado diversas estrategias  para la determinación de esta métrica, sin embargo en el mundo digital estos procesos se han simplificado considerablemente, siendo la técnica del borde inclinado (slant edge) una de las más sencillas de llevar a cabo, descrita entre otras técnicas en la ISO 12233:2000 Photography Electronic still picture cameras Resolution measurements.
La estrategia del borde-inclinado consiste en generar imágenes sobre nuestro sensor donde exista un borde correctamente diferenciado, con una orientación vertical y una ligera inclinación (aprox 5-10º), de forma que sea posible determinar la SFR (Spatial Frequency Response)  horizontal.

Para el cálculo es necesario contar con alguna herramienta que nos permita realizar cálculos de este tipo, podemos recurrir a herramientas comerciales como Imatest o FRAME, pero para nuestros propósitos será más que suficiente el plugin de ImageJ, desarrollado por el profesor de fotografía de la UPC Carles Mitja  denominado “Slanted Edge MTF”, que nos arrojará información básica sobre los aspectos de la MTF, como alternativa a este plugin también esta disponible para ImageJ el trabajo de Jeffrey Kuhn “Modulation Transfer Function”.

La carta de resolución las podemos adquirir, pero también las podemos imprimir nosotros mismos. La carta estandard de de la ISO 12233 se puede descargar desde la universidad de Cornell .Al imprimir una de estas cartas, o cualquier forma que presente un borde inclinado, hay que prestar mucha atención a precisión del borde ya que muchos sistemas de inyección de tinta suelen crear bordes poco precisos. Quizás la impresión en papel cromogénico (Lambda) nos ofrece unos resultados bastante óptimos. Hay que prestar mucha atención a las particularidades de la carta, pero también a los procesos de corrección electrónica de la imagen, ya que estos condicionan o se ven reflejados en la MTF

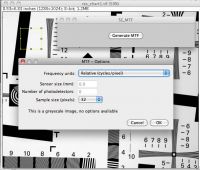Antes de llamar al plugin a través de Plugins > Analyze > SE MTF 2xNyquist, debemos determinar nuestra ROI (region of interest) o área a estudiar, mediante la característica selección rectangular de imageJ.

El uso del plugin de Carles es bastante intuitivo de usar, basta con dejar ajustadas las opciones por defecto:

Frecuency units: Relative (cycles/Pixel)
Sample Size: 32

Si la imagen esta en escala de grises ya no hay más opciones disponibles, sin embargo si se trata de una imagen RGB podemos calcular la MTF por cada canal o el promedio de los tres.

Al activar el proceso de cálculo se despliegan cuatro ventanas:

• MTF - Modulation transfer funcion
• ESF - Edge Spread Funcion
• LSF - Line Spread Function
• SPP - Sampling Periodicity Plot

A partir de aquí el proceso se complica ya que la compresión de estas gráficas no acaba de ser sencillo y sólo la experiencia de visualizar y comparar muchas nos puede dar un cierto entendimiento de lo que esta sucediendo.

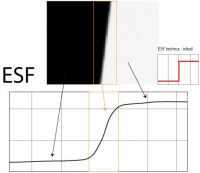El gráfico ESF es la primera fase del proceso, el cual constituye la representación gráfica de nuestro borde o transición entre la zona negra y la blanca de nuestra figura. Este gráfico suele presentarse como una especie de curva donde la parte inferior indica la zona negra de nuestra carta, la superior la zona blanca, y la pendiente que las une la transición entre ambas, de forma que cuanto más pronunciada es dicha pendiente más contraste, y por tanto definición existe en nuestro borde.

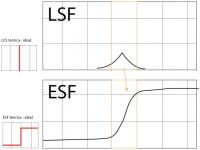La LSF se deduce de la ESF de forma que suele presentarse como un gráfico con un pico  que se desarrolla a lo largo del eje de abcisas. Cuanto más preciso es nuestro borde más estrecho y alto suele ser este pico.

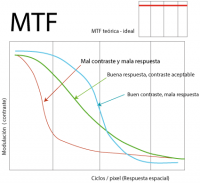De estas dos procesos se deduce la MTF, la cual suele ser una gráfica con una característica curva en forma de S poco pronunciada, de forma que el contraste se decrece a medida que se reduce la respuesta espacial. En este punto existen pocas estrategias para la interpretación en términos absolutos de dichas curvas, quizás una tendencia hacia los valores teóricos ideales, o el área de la curva, ya que en términos generales a mayor área mayor calidad. En la imagen que acompaña este gráfico se indican algunas propuestas que nos pueden resultar de utilidad para una aproximación a la interpretación de las MTF.